電気の資格のアレコレ
第二種電気工事士 筆記試験 計算問題を完全攻略せよ その２ 「過去問を解説編」
更新日：2022.07.12投稿日：2022.07.12
SHARE
その１では覚えるべき公式について解説しました。ここからは応用編。過去問を一緒に解いていきましょう。
合成抵抗を求める問題１
過去問自体は「電気技術者試験センター」のサイトに掲載されています。こちらもぜひ活用してください。
試験の問題と解答 | ECEE 一般財団法人電気技術者試験センター
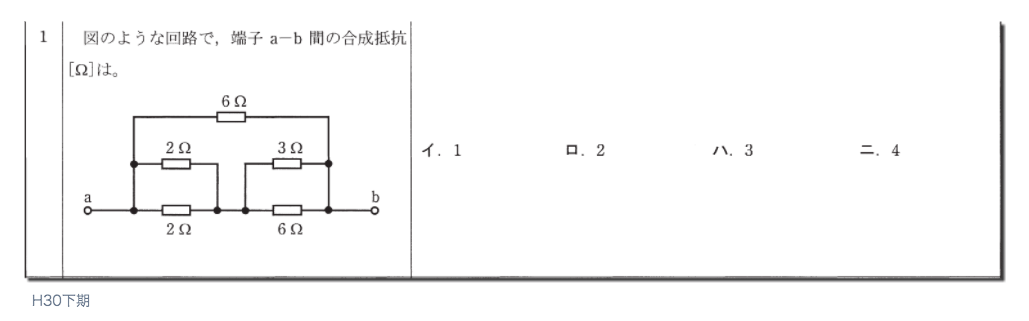
一見難しそうに感じますが、直列と並行の合成抵抗計算の解き方で解けます。
まず、左下の2Ωと2Ωが並列に繋がっている箇所がありますが、こちらを並行回路の求め方で求めると （2Ω×2Ω）÷（2Ω+2Ω）＝4÷4＝1 となります。
次に、右側の3Ωと6Ωも同じように求めると （3×6）÷（3+6）＝18÷9＝2Ωこの二つを求めると、左側と右側で直接回路になるのでそのまま足します。
1+2＝3Ω
合成抵抗を求める問題２
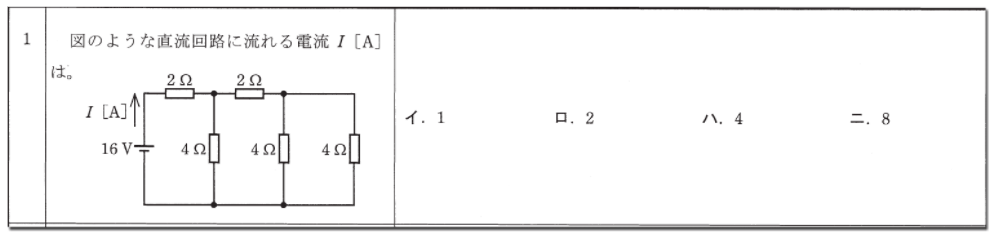
まず、右側の4Ωと4Ωを並列回路で求めると（4×4）÷（4+4）＝2Ω
次にそのすぐ左上の抵抗2Ωと今度は直列になるので足しましょう。 2+2＝4
そして、その横の4Ωとまた並列となるので （4×4）÷（4+4）＝2Ω と求め、再びその左上の抵抗と直列になるので足していきます。 2+2＝4Ω
次に電流を求めます。Ｖ＝ＲIという公式に当てはめて計算しましょう。
Ｖ＝16ですから、
16＝Ｉ×4、I＝4
となり、答えは「ハ」となります。
電圧を求める問題
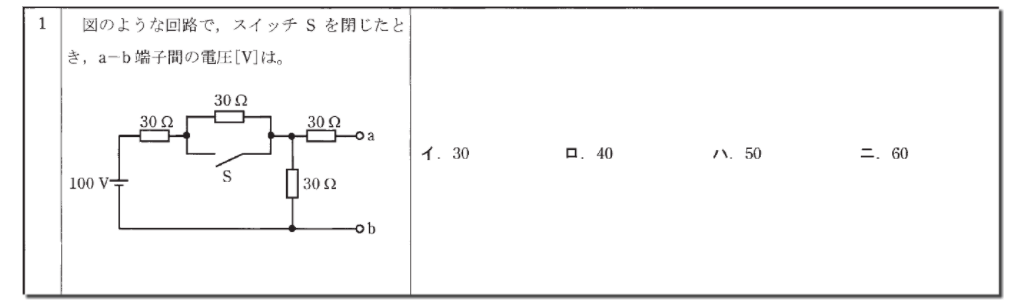
スイッチＳを閉じると、抵抗は小さい方に流れるので閉じた方は抵抗がないため、こちらに電流が流れます。次にaの横の30Ωですが、aの地点のように途切れている回路には電流が流れません。
この2点を考慮すると、スイッチSの上の30Ωとaの横の30Ωは無視できます（ここが重要です）
残った30Ωが2つ直列に繋がった状態で残ります。
ここで、分圧という言葉が出てきますが、純粋に全体の電圧を各抵抗（今回は同じ抵抗値）で分散するだけなので、計算は
100÷2＝50となり、答えは「ハ」となります。
この記事をシェアする：
この記事を書いた人
一覧に戻る
関連のある記事
